Unsupervised Learning to Solve Inverse Problems

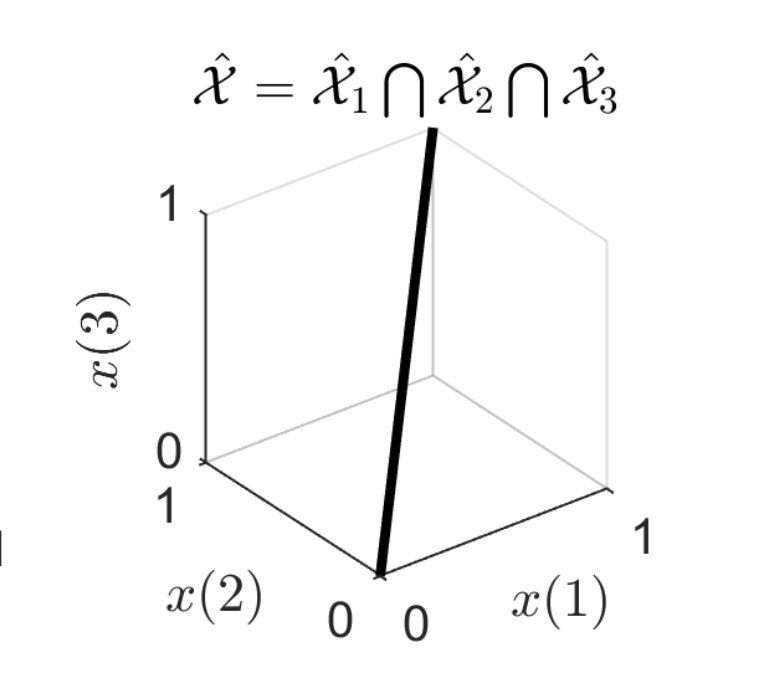
Inverse problems are ubiquitous in signal and image processing. In most applications, we need to reconstruct an underlying signal \(x\in\mathbb{R}^{n}\), from some measurements \(y\in\mathbb{R}^{m}\), that is, invert the forward measurement process, \begin{equation} y = Ax+n \end{equation} where \(n\) represents some noise and \(A\) is the forward operator. Due to the ill-posed nature of \(A\) (we generally have \(m<n\)) and noise, there are multiple possible solutions \(x\) for a given \(y\). Fortunately, the set of plausible (natural) signals \(x\) lie in a small low-dimensional set \(\mathcal{X}\) of the whole of \(\mathbb{R}^{n}\), so we can have a unique \(x\) for a given \(y\).

The traditional approach is to build a mathematical model to describe \(\mathcal{X}\) leveraging some prior knowledge about the underlying signals (e.g. natural images can be described as piecewise smooth). However, this a hard task which is problem-dependent and it is generally a loose description of the true \(\mathcal{X}\).

In recent years, an alternative approach is to learn inverse mapping from \(y\mapsto x\) directly from training data, bypassing the need to design a prior model. Fuelled by the powerful learning bias of deep convolutional neural networks (interest readers can have a look at my previous post about understanding this implicit bias), the goal is to learn a function \(x=f(y)\) from training pairs \((x_i,y_i)\). The fundamental limitation of this approach is that in many real world applications we can only access \(y\). Training only with the \(y_i\) (enforcing measurement consistency) accounts to finding an \(f\) such that \(y=A f(y)\). Unfortunately this is doomed to fail, as there are infinite possible functions \(f\) that can fit the measurements perfectly well! This is because any \(f\) can output any value in the nullspace of \(A\) and still achieve measurement consistency. In other words, this fundamental limitation is a chicken-and-egg problem: we cannot learn to solve an inverse problem without solving it first to obtain the ground-truth training data!

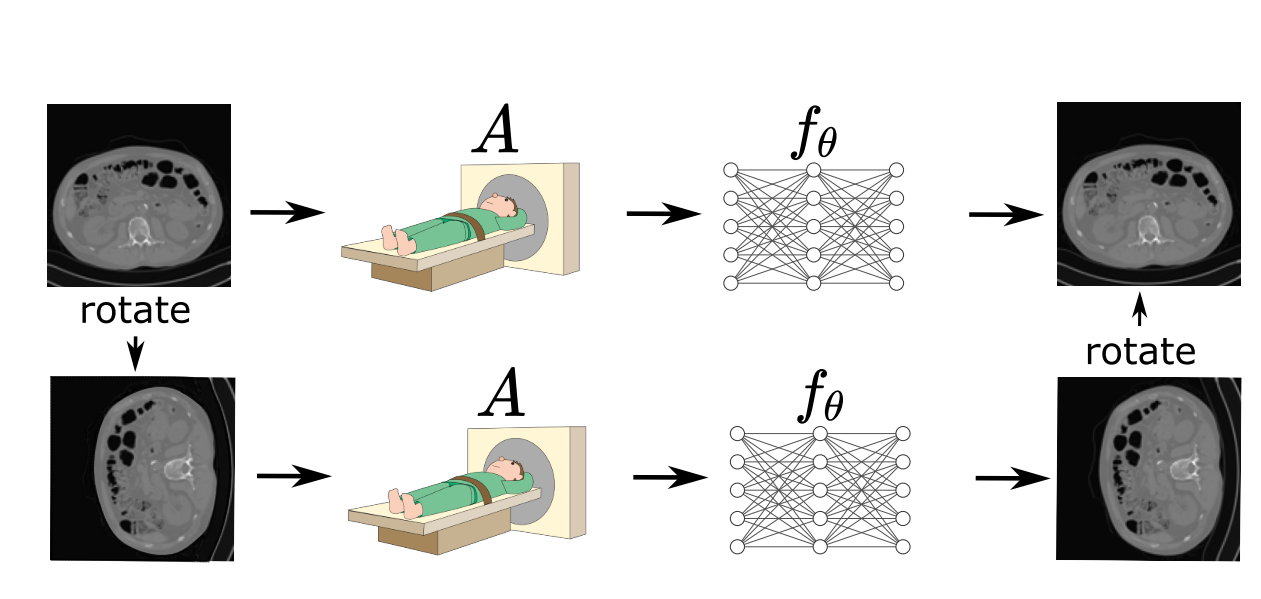
In (Chen et al., 2021), we show that this problem can be overcome by adding a small assumption to the underlying set of signals \(\mathcal{X}\): invariance. It is well-known that most natural signals posses some kind of invariance. For example, images are generally invariant to shifts or rotations. Hence, the whole sensing process \(x = (f \circ A) (x)\) is necessarily an equivariant function, that is, given a transformation \(T_g\) (e.g. a shift), we have that \begin{equation} T_gx = (f\circ A) (T_gx). \end{equation} The invariance gives us information of the nullspace of A, which boils down to the following observation: \begin{equation} y=Ax = AT_g x’ = A_g x’ \end{equation} which just relies on the fact that \(x'= T_gx\) is another valid signal. Hence we can see beyond the range space of \(A\), as we have an implicit access to multiple different operators \(A_g = AT_g\) for all possible transformations \(T_1,\dots,T_{G}\).

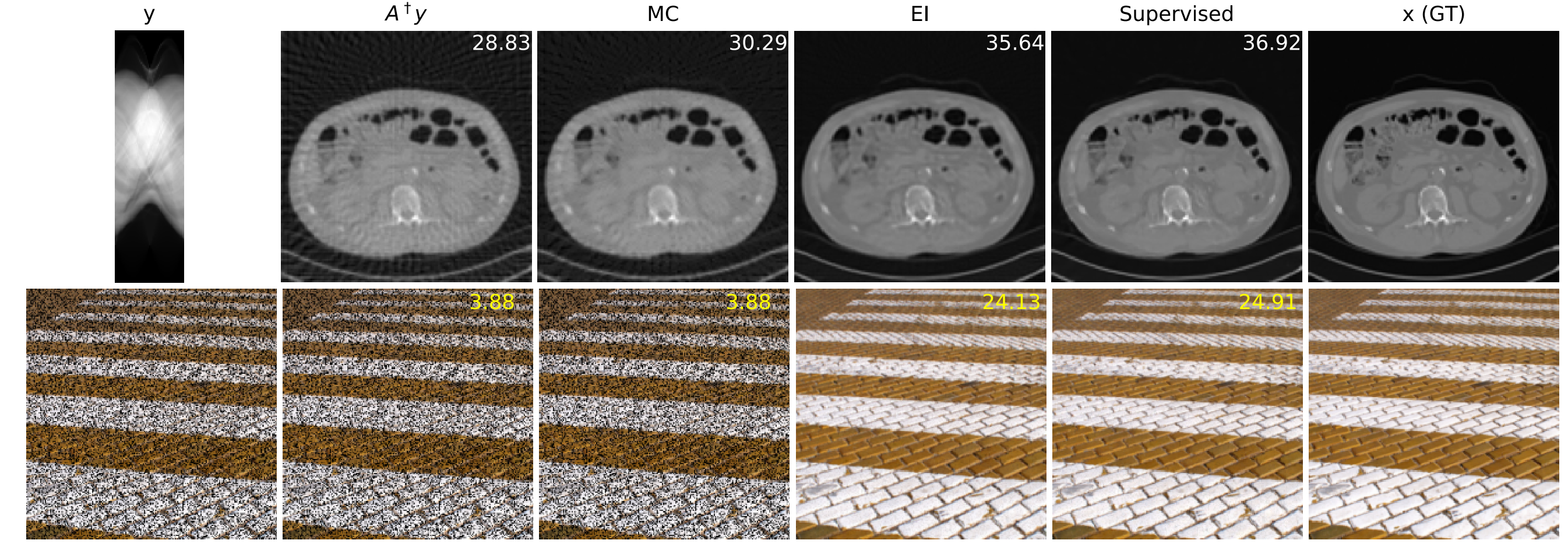
Learning to image from only measurements. Training an imaging network through just measurement consistency (MC) does not significantly improve the reconstruction over the simple pseudo-inverse. However, by enforcing invariance in the reconstructed image set, equivariant imaging (EI) performs almost as well as a fully supervised network. Top: sparse view CT reconstruction, Bottom: pixel inpainting. PSNR is shown in top right corner of the images

(Chen et al., 2021) shows that the invariance constraint on \((f\circ A)\) can be easily incorporated as an additional loss term when training a deep network. In (Chen et al., 2022) we extended the unsupervised method to account for noise. The method builds an unsupervised loss using Stein’s unbiased risk (SURE) estimator, which approximates the noiseless measurement consistency.

Experiments in (Chen et al., 2021) and (Chen et al., 2021) show that for the computed tomography and inpaiting problems, the equivariant learning approach (only having access to measurements \(y_i\)) performs as well as the fully supervised case i.e. having training pairs with ground-truth data \((x_i,y_i)\), by-passing the fundamental limitation of learning to solve inverse problems.

Theory

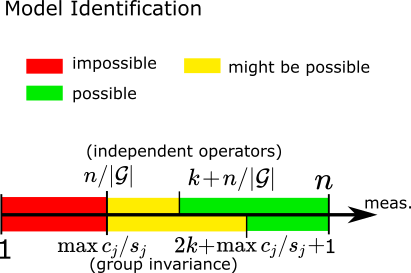
Despite the good empirical results, a few important theoretical questions arise: When is unsupervised learning possible? How big has the group invariance has to be? How many measurements per observation do we need?

We provide answers to these questions in (Tachella et al., 2023):

Necessary Conditions

In order to learn from measurement data alone, we need that the set range spaces of virtual operators span the full ambient space \(\mathbb{R}^{n}\), i.e.,

\[\begin{equation}\label{eq:necessary} \text{rank}\begin{bmatrix} AT_1 \\ \vdots \\ AT_G \end{bmatrix} = n \end{equation}\]

This condition requires that \(m \geq \max_j c_j/s_j\) where \({s_j}\) and \({c_j}\) are the dimension and multiplicities of the irreducible representations of the group action. Most group symmetries (translations, reflections or rotations of a signal) appearing in practice have \(\max_j c_j/s_j=n/G\). In this case, we need at least \begin{equation} m \geq n/G \end{equation} measurements.

Moreover, condition \eqref{eq:necessary} requires that the forward operator \(A\) is not equivariant to the group action. Otherwise, the concatenation of \(AT_1,\dots, AT_{G}\) has rank \(m<n\).

Sufficient Condition

In order to guarantee unique model recovery, we need to take into account the dimension of the signal set \(\mathcal{X}\). Let \(k\) be the box-counting dimension of \(\mathcal{X}\) and let \(G\) be a cyclic group where \(\{c_j\}\) denote th multiplicities of the irreducible representations. Then, almost every forward operator \(A\in \mathbb{R}^{m\times n}\) with \(m> 2k + 1 + \max_j c_j\). Most cyclic group symmetries (translations, reflections or rotations of a signal) appearing in practice have \(\max_j c_j=n/G\). In these cases we have that fully self-supervised learning is possible by almost every \(A\) with \begin{equation} m> 2k + 1 + n/G \end{equation} measurements.

Multiple operators

If the signal set is not group invariant, but we observe measurements via different operators \(A_1,\dots,A_G\), then unsupervised from measurement data alone is possible. In this case the necessary condition on the number of measurements is \(m\geq n/G\), and the sufficient condition is \(m>n/G+k\). These results are included in (Tachella et al., 2022).

2023

Sensing Theorems for Unsupervised Learning in Linear Inverse Problems

Julian Tachella, Dongdong Chen , and Mike Davies

Journal of Machine Learning Research (JMLR), Jan 2023

Abs arXiv PDF

Solving a linear inverse problem requires knowledge about the underlying signal model. In many applications, this model is a priori unknown and has to be learned from data. However, it is impossible to learn the model using observations obtained via a single incomplete measurement operator, as there is no information outside the range of the inverse operator, resulting in a chicken-and-egg problem: to learn the model we need reconstructed signals, but to reconstruct the signals we need to know the model. Two ways to overcome this limitation are using multiple measurement operators or assuming that the signal model is invariant to a certain group action. In this paper, we present necessary and sufficient sensing conditions for learning the signal model from partial measurements which only depend on the dimension of the model, and the number of operators or properties of the group action that the model is invariant to. As our results are agnostic of the learning algorithm, they shed light into the fundamental limitations of learning from incomplete data and have implications in a wide range set of practical algorithms, such as dictionary learning, matrix completion and deep neural networks.

2022

Robust Equivariant Imaging: a fully unsupervised framework for learning to image from noisy and partial measurements

Dongdong Chen , Julian Tachella, and Mike E Davies

Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun 2022

Abs arXiv Video Code

Deep networks provide state-of-the-art performance in multiple imaging inverse problems ranging from medical imaging to computational photography. However, most existing networks are trained with clean signals which are often hard or impossible to obtain. Equivariant imaging (EI) is a recent self-supervised learning framework that exploits the group invariance present in signal distributions to learn a reconstruction function from partial measurement data alone. While EI results are impressive, its performance degrades with increasing noise. In this paper, we propose a Robust Equivariant Imaging (REI) framework which can learn to image from noisy partial measurements alone. The proposed method uses Stein’s Unbiased Risk Estimator (SURE) to obtain a fully unsupervised training loss that is robust to noise. We show that REI leads to considerable performance gains on linear and nonlinear inverse problems, thereby paving the way for robust unsupervised imaging with deep networks.
Unsupervised Learning From Incomplete Measurements for Inverse Problems

Julian Tachella, Dongdong Chen , and Mike Davies

NeurIPS 2022, May 2022

Abs arXiv Code

In many real-world inverse problems, only incomplete measurement data are available for training which can pose a problem for learning a reconstruction function. Indeed, unsupervised learning using a fixed incomplete measurement process is impossible in general, as there is no information in the nullspace of the measurement operator. This limitation can be overcome by using measurements from multiple operators. While this idea has been successfully applied in various applications, a precise characterization of the conditions for learning is still lacking. In this paper, we fill this gap by presenting necessary and sufficient conditions for learning the underlying signal model needed for reconstruction which indicate the interplay between the number of distinct measurement operators, the number of measurements per operator, the dimension of the model and the dimension of the signals. Furthermore, we propose a novel and conceptually simple unsupervised learning loss which only requires access to incomplete measurement data and achieves a performance on par with supervised learning when the sufficient condition is verified. We validate our theoretical bounds and demonstrate the advantages of the proposed unsupervised loss compared to previous methods via a series of experiments on various imaging inverse problems, such as accelerated magnetic resonance imaging, compressed sensing and image inpainting.

2021

Equivariant Imaging: Learning Beyond the Range Space

Dongdong Chen , Julian Tachella, and Mike E Davies

In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) , Mar 2021

Abs PDF Video Code

In various imaging problems, we only have access to compressed measurements of the underlying signals, hindering most learning-based strategies which usually require pairs of signals and associated measurements for training. Learning only from compressed measurements is impossible in general, as the compressed observations do not contain information outside the range of the forward sensing operator. We propose a new end-to-end self-supervised framework that overcomes this limitation by exploiting the equivariances present in natural signals. Our proposed learning strategy performs as well as fully supervised methods. Experiments demonstrate the potential of this framework on inverse problems including sparse-view X-ray computed tomography on real clinical data and image inpainting on natural images.