Unsupervised Learning to Solve Inverse Problems
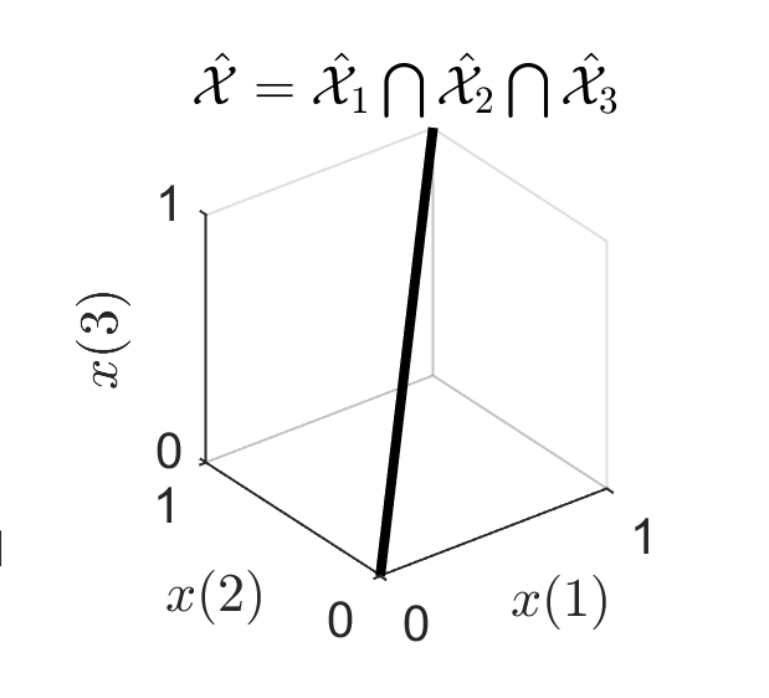
Inverse problems are ubiquitous in signal and image processing. In most applications, we need to reconstruct an underlying signal \(x\in\mathbb{R}^{n}\), from some measurements \(y\in\mathbb{R}^{m}\), that is, invert the forward measurement process, \begin{equation} y = Ax+n \end{equation} where \(n\) represents some noise and \(A\) is the forward operator. Due to the ill-posed nature of \(A\) (we generally have \(m<n\)) and noise, there are multiple possible solutions \(x\) for a given \(y\). Fortunately, the set of plausible (natural) signals \(x\) lie in a small low-dimensional set \(\mathcal{X}\) of the whole of \(\mathbb{R}^{n}\), so we can have a unique \(x\) for a given \(y\).
The traditional approach is to build a mathematical model to describe \(\mathcal{X}\) leveraging some prior knowledge about the underlying signals (e.g. natural images can be described as piecewise smooth). However, this a hard task which is problem-dependent and it is generally a loose description of the true \(\mathcal{X}\).
In recent years, an alternative approach is to learn inverse mapping from \(y\mapsto x\) directly from training data, bypassing the need to design a prior model. Fuelled by the powerful learning bias of deep convolutional neural networks (interest readers can have a look at my previous post about understanding this implicit bias), the goal is to learn a function \(x=f(y)\) from training pairs \((x_i,y_i)\). The fundamental limitation of this approach is that in many real world applications we can only access \(y\). Training only with the \(y_i\) (enforcing measurement consistency) accounts to finding an \(f\) such that \(y=A f(y)\). Unfortunately this is doomed to fail, as there are infinite possible functions \(f\) that can fit the measurements perfectly well! This is because any \(f\) can output any value in the nullspace of \(A\) and still achieve measurement consistency. In other words, this fundamental limitation is a chicken-and-egg problem: we cannot learn to solve an inverse problem without solving it first to obtain the ground-truth training data!
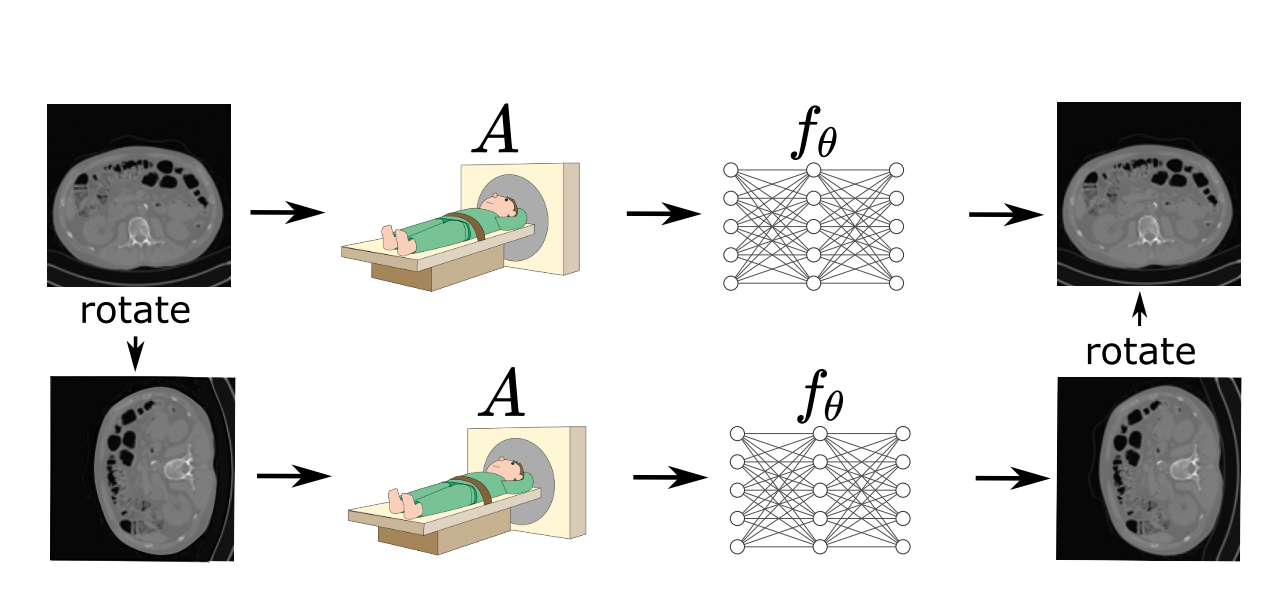
In (Chen et al., 2021), we show that this problem can be overcome by adding a small assumption to the underlying set of signals \(\mathcal{X}\): invariance. It is well-known that most natural signals posses some kind of invariance. For example, images are generally invariant to shifts or rotations. Hence, the whole sensing process \(x = (f \circ A) (x)\) is necessarily an equivariant function, that is, given a transformation \(T_g\) (e.g. a shift), we have that \begin{equation} T_gx = (f\circ A) (T_gx). \end{equation} The invariance gives us information of the nullspace of A, which boils down to the following observation: \begin{equation} y=Ax = AT_g x’ = A_g x’ \end{equation} which just relies on the fact that \(x'= T_gx\) is another valid signal. Hence we can see beyond the range space of \(A\), as we have an implicit access to multiple different operators \(A_g = AT_g\) for all possible transformations \(T_1,\dots,T_{G}\).
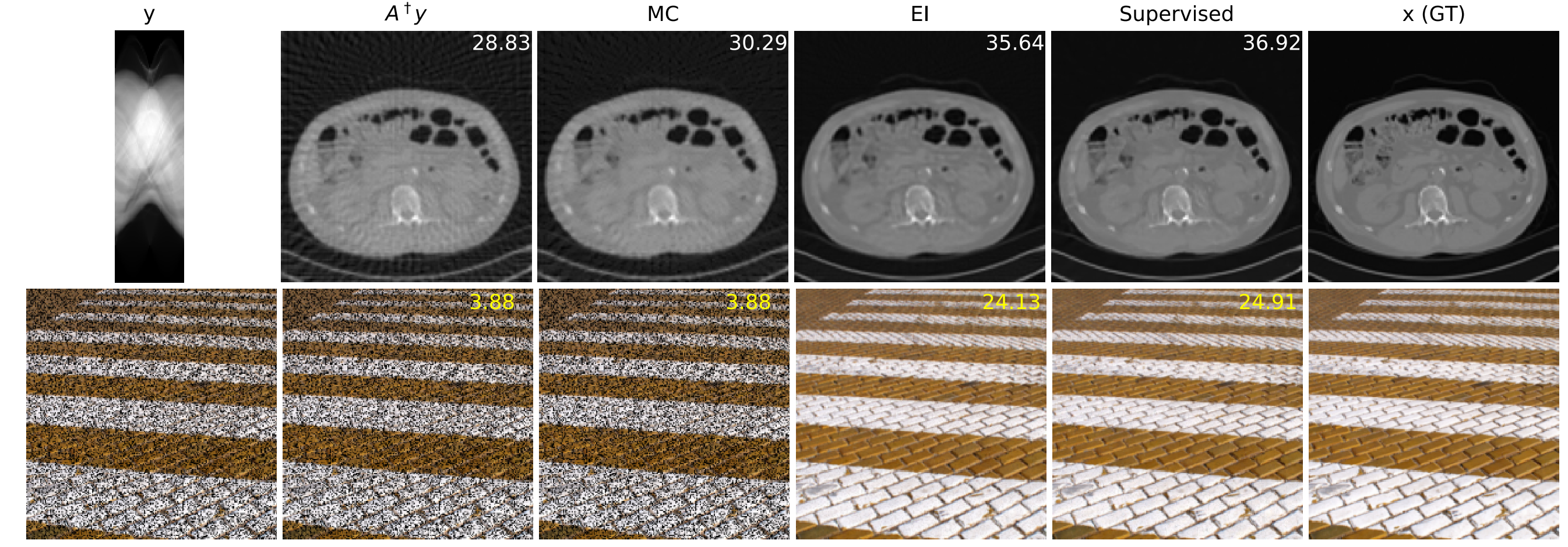
(Chen et al., 2021) shows that the invariance constraint on \((f\circ A)\) can be easily incorporated as an additional loss term when training a deep network. In (Chen et al., 2022) we extended the unsupervised method to account for noise. The method builds an unsupervised loss using Stein’s unbiased risk (SURE) estimator, which approximates the noiseless measurement consistency.
Experiments in (Chen et al., 2021) and (Chen et al., 2021) show that for the computed tomography and inpaiting problems, the equivariant learning approach (only having access to measurements \(y_i\)) performs as well as the fully supervised case i.e. having training pairs with ground-truth data \((x_i,y_i)\), by-passing the fundamental limitation of learning to solve inverse problems.
Theory
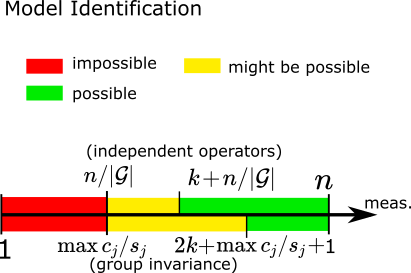
Despite the good empirical results, a few important theoretical questions arise: When is unsupervised learning possible? How big has the group invariance has to be? How many measurements per observation do we need?
We provide answers to these questions in (Tachella et al., 2023):
Necessary Conditions
In order to learn from measurement data alone, we need that the set range spaces of virtual operators span the full ambient space \(\mathbb{R}^{n}\), i.e.,
\[\begin{equation}\label{eq:necessary} \text{rank}\begin{bmatrix} AT_1 \\ \vdots \\ AT_G \end{bmatrix} = n \end{equation}\]This condition requires that \(m \geq \max_j c_j/s_j\) where \({s_j}\) and \({c_j}\) are the dimension and multiplicities of the irreducible representations of the group action. Most group symmetries (translations, reflections or rotations of a signal) appearing in practice have \(\max_j c_j/s_j=n/G\). In this case, we need at least \begin{equation} m \geq n/G \end{equation} measurements.
Moreover, condition \eqref{eq:necessary} requires that the forward operator \(A\) is not equivariant to the group action. Otherwise, the concatenation of \(AT_1,\dots, AT_{G}\) has rank \(m<n\).
Sufficient Condition
In order to guarantee unique model recovery, we need to take into account the dimension of the signal set \(\mathcal{X}\). Let \(k\) be the box-counting dimension of \(\mathcal{X}\) and let \(G\) be a cyclic group where \(\{c_j\}\) denote th multiplicities of the irreducible representations. Then, almost every forward operator \(A\in \mathbb{R}^{m\times n}\) with \(m> 2k + 1 + \max_j c_j\). Most cyclic group symmetries (translations, reflections or rotations of a signal) appearing in practice have \(\max_j c_j=n/G\). In these cases we have that fully self-supervised learning is possible by almost every \(A\) with \begin{equation} m> 2k + 1 + n/G \end{equation} measurements.
Multiple operators
If the signal set is not group invariant, but we observe measurements via different operators \(A_1,\dots,A_G\), then unsupervised from measurement data alone is possible. In this case the necessary condition on the number of measurements is \(m\geq n/G\), and the sufficient condition is \(m>n/G+k\). These results are included in (Tachella et al., 2022).